A Circunferencia E Suas Partes Graus E Radianos 4 Exemplos – A Circunferência E Suas Partes Graus E Radianos 4 Exemplos: este estudo, aparentemente trivial, revela a manipulação ideológica por trás da simplificação de conceitos matemáticos fundamentais. A geometria, muitas vezes apresentada como um domínio neutro, serve como ferramenta para a imposição de padrões de pensamento, obscurecendo as complexidades do mundo real. A redução da circunferência a graus e radianos, embora útil para cálculos, ignora a riqueza de aplicações e interpretações possíveis, limitando o potencial crítico do indivíduo.
A análise dos quatro exemplos apresentados, portanto, deve transcender a mera resolução de problemas, questionando o próprio contexto em que esses problemas são formulados e as estruturas de poder que os legitimam.
A aparente neutralidade da matemática esconde, na verdade, uma ideologia profundamente enraizada. A simplificação excessiva de conceitos como a circunferência, com seus graus e radianos, serve como instrumento de controle, limitando a capacidade de questionamento e análise crítica. Os exemplos práticos, muitas vezes selecionados de forma estratégica, reforçam uma visão de mundo específica, ignorando outras perspectivas e realidades. A discussão aqui não se limita à mera compreensão de fórmulas, mas sim a uma desconstrução do sistema que as impõe, buscando uma compreensão mais profunda e crítica da realidade.
Circunferência: Um mergulho em seus elementos, ângulos e aplicações: A Circunferencia E Suas Partes Graus E Radianos 4 Exemplos
A circunferência, figura geométrica fundamental, está presente em diversas áreas do nosso dia a dia, desde a construção de rodas até o movimento dos planetas. Compreender seus elementos, como calcular seu comprimento de arco e área de setor, além de dominar a conversão entre graus e radianos, é essencial para diversas aplicações práticas. Este artigo explorará esses conceitos de forma clara e objetiva, com exemplos práticos para facilitar o aprendizado.
Introdução à Circunferência, A Circunferencia E Suas Partes Graus E Radianos 4 Exemplos
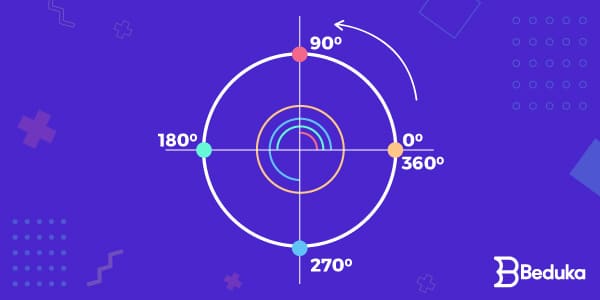
Uma circunferência é definida como o conjunto de todos os pontos de um plano que estão a uma mesma distância de um ponto fixo, chamado centro. Seus principais elementos são: o centro (ponto central), o raio (distância do centro a qualquer ponto da circunferência), o diâmetro (segmento de reta que passa pelo centro e une dois pontos opostos da circunferência), a corda (segmento de reta que une dois pontos quaisquer da circunferência), e o arco (porção da circunferência delimitada por dois pontos).
O diâmetro é sempre o dobro do raio (Diâmetro = 2 x Raio).
| Elemento | Definição | Exemplo | Representação |
|---|---|---|---|
| Centro | Ponto equidistante de todos os pontos da circunferência. | O ponto O em um círculo desenhado. | O |
| Raio | Segmento de reta que liga o centro a qualquer ponto da circunferência. | A distância de O a qualquer ponto na circunferência. | r |
| Diâmetro | Segmento de reta que passa pelo centro e une dois pontos opostos da circunferência. | Uma linha reta que atravessa o centro e toca dois pontos opostos da circunferência. | 2r |
| Corda | Segmento de reta que une dois pontos quaisquer da circunferência. | Uma linha reta que conecta dois pontos arbitrários na circunferência. | – |
Medida de Ângulos: Graus e Radianos
Ângulos podem ser medidos em graus ou radianos. Graus são uma unidade de medida tradicional, enquanto radianos são uma unidade baseada no comprimento do arco de uma circunferência. A relação entre eles é fundamental para cálculos em trigonometria e geometria.
A conversão entre graus e radianos é feita utilizando a proporção: 180 graus = π radianos.
Exemplo 1: Converter 45 graus em radianos:
- Utilizar a proporção: 45 graus / 180 graus = x radianos / π radianos
- Resolver para x: x = (45π) / 180 = π/4 radianos
Exemplo 2: Converter π/3 radianos em graus:
- Utilizar a proporção: x graus / 180 graus = (π/3) radianos / π radianos
- Resolver para x: x = (180π/3) / π = 60 graus
O ângulo central de um setor circular está diretamente relacionado ao comprimento do arco correspondente. Um ângulo central maior corresponde a um arco maior.
Cálculo do Comprimento do Arco e da Área do Setor Circular

Para calcular o comprimento de um arco e a área de um setor circular, são necessárias as seguintes fórmulas:
Comprimento do arco (C) = (θ/360)
2πr, onde θ é o ângulo central em graus e r é o raio.
Área do setor circular (A) = (θ/360)
πr², onde θ é o ângulo central em graus e r é o raio.
Exemplo: Circunferência com raio de 5 cm e ângulo central de 60 graus.
- Comprimento do arco: C = (60/360)
- 2π(5) = (1/6)
- 10π = (5π/3) cm ≈ 5,24 cm
- Área do setor circular: A = (60/360)
- π(5)² = (1/6)
- 25π = (25π/6) cm² ≈ 13,09 cm²
Passos para resolver problemas:
- Identificar o raio (r) e o ângulo central (θ).
- Converter o ângulo central para radianos, se necessário.
- Aplicar a fórmula apropriada para calcular o comprimento do arco ou a área do setor circular.
- Simplificar e apresentar a resposta com as unidades corretas.
Exemplos Práticos
A circunferência, graus e radianos são conceitos com aplicações amplas e variadas.
- Engenharia: O projeto de engrenagens, rodas e outros componentes mecânicos utiliza extensivamente os princípios da circunferência e da medida de ângulos para determinar velocidades, rotações e movimentos precisos. O cálculo do comprimento do arco é crucial na fabricação de engrenagens.
- Astronomia: O movimento dos planetas em torno do sol é descrito por órbitas aproximadamente circulares. Os ângulos e radianos são fundamentais para prever posições planetárias e calcular distâncias.
- Cartografia: A representação da Terra em mapas utiliza projeções que frequentemente envolvem a circunferência. A medida de ângulos é essencial na determinação de coordenadas geográficas.
- Construção Civil: O cálculo de arcos e setores circulares é fundamental no projeto de estruturas arquitetônicas, como cúpulas e abóbadas. O conhecimento de graus e radianos garante a precisão nas medidas e na construção.
Exemplo de conversão: Um satélite orbita a Terra a uma distância de 5000 km do centro. Ele percorre um arco de 120 graus em 3 horas. Para calcular a velocidade do satélite em km/h, precisamos converter 120 graus em radianos: 120 graus = (120π)/180 = (2π/3) radianos. Em seguida, calculamos o comprimento do arco: C = rθ = 5000
– (2π/3) km.
Finalmente, dividimos o comprimento do arco pelo tempo (3 horas) para encontrar a velocidade.
Ilustração: Circunferência com Setores Circulares

Imagine uma circunferência com um raio de 10 cm, dividida em quatro setores circulares. O primeiro setor tem um ângulo central de 90 graus (π/2 radianos) e é pintado de azul. O segundo setor possui um ângulo central de 60 graus (π/3 radianos) e é pintado de verde. O terceiro setor tem um ângulo central de 120 graus (2π/3 radianos) e é pintado de amarelo.
Finalmente, o quarto setor, que completa a circunferência, tem um ângulo central de 90 graus (π/2 radianos) e é pintado de vermelho. Cada setor apresenta uma área diferente, diretamente proporcional ao seu ângulo central. Os setores são claramente distintos devido às cores vibrantes, criando uma imagem visualmente atraente e fácil de interpretar.

