Equação do 2º Grau: Fatoração: Equação Do 2 Grau Como Fazer Pelo Metodo Fatoração Exemplo
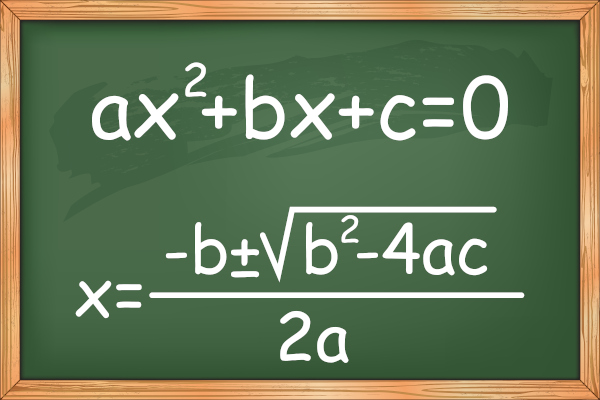
Equação Do 2 Grau Como Fazer Pelo Metodo Fatoração Exemplo – A equação do segundo grau é uma ferramenta fundamental na matemática, com aplicações em diversas áreas, desde a física e engenharia até a economia e finanças. Resolver uma equação do segundo grau significa encontrar os valores da variável que tornam a equação verdadeira. Um dos métodos mais eficazes para resolver equações do segundo grau é a fatoração, um processo algébrico que decompõe a equação em fatores mais simples, facilitando a identificação das raízes.
Introdução à Equação do 2º Grau
Uma equação do segundo grau é uma equação polinomial de grau dois, que pode ser representada na sua forma geral como: ax² + bx + c = 0, onde a, b, e c são coeficientes reais, com a diferente de zero (a ≠ 0). O coeficiente a determina a concavidade da parábola que representa graficamente a equação; b influencia a posição do vértice; e c representa o ponto de interseção com o eixo y.
Vejamos alguns exemplos:
| Equação | a | b | c | Classificação |
|---|---|---|---|---|
| 2x² + 5x + 3 = 0 | 2 | 5 | 3 | Completa |
| x² – 9 = 0 | 1 | 0 | -9 | Incompleta (Pura) |
| 3x² + 6x = 0 | 3 | 6 | 0 | Incompleta (Mista) |
| -x² + 4x – 4 = 0 | -1 | 4 | -4 | Completa |
Método da Fatoração: Conceitos Básicos
A fatoração, aplicada à resolução de equações do segundo grau, consiste em reescrever a equação como um produto de dois ou mais fatores. As raízes da equação são os valores que, quando substituídos na variável x, tornam cada fator igual a zero. Em comparação com outros métodos, como a fórmula de Bhaskara, a fatoração oferece uma solução mais direta e elegante, quando aplicável.
Entretanto, nem todas as equações do segundo grau podem ser resolvidas facilmente por fatoração.
Exemplo passo a passo da fatoração de uma equação simples: x²
-5x + 6 = 0
- Encontre dois números que, somados, resultem em -5 (coeficiente de x) e, multiplicados, resultem em 6 (termo constante).
- Esses números são -2 e -3. (-2 + (-3) = -5 e (-2) – (-3) = 6).
- Reescreva a equação na forma fatorada: (x – 2)(x – 3) = 0
- Resolva cada fator igualando-o a zero: x – 2 = 0 => x = 2; x – 3 = 0 => x = 3
- As raízes da equação são x = 2 e x = 3.
Fatoração de Equações do 2º Grau: Exemplos Práticos
Vamos analisar exemplos práticos de resolução de equações do segundo grau completas e incompletas usando o método da fatoração.
Equação completa: 2x² + 7x + 3 = 0
- Procurar dois números que somados resultam em 7 e multiplicados resultam em 6 (2*3=6).
- Esses números são 6 e 1.
- Reescrever a equação como: 2x² + 6x + x + 3 = 0
- Fatorar por agrupamento: 2x(x+3) + 1(x+3) = 0
- Fatorar novamente: (2x+1)(x+3) = 0
- As raízes são: x = -3 e x = -1/2
A fatoração por agrupamento é útil quando a equação não se encaixa diretamente na forma (x+a)(x+b)=0.
Equação incompleta (pura): x²
-16 = 0
Essa equação pode ser resolvida utilizando a diferença de quadrados:
- Reescrever como: (x – 4)(x + 4) = 0
- As raízes são: x = 4 e x = -4
| Equação | Tipo | Fatoração | Raízes |
|---|---|---|---|
| x² – 25 = 0 | Incompleta (Pura) | (x-5)(x+5) = 0 | x = 5, x = -5 |
| 3x² – 6x = 0 | Incompleta (Mista) | 3x(x-2) = 0 | x = 0, x = 2 |
Casos Especiais na Fatoração

Existem casos onde a fatoração direta não é possível, como em equações que não possuem raízes reais. Neste caso, o discriminante (Δ = b²
-4ac) da equação será negativo. Equações com raízes repetidas (raízes iguais) podem ser fatoradas, resultando em um fator ao quadrado. A possibilidade de fatoração depende diretamente dos coeficientes a, b e c, sendo mais fácil quando os coeficientes são números inteiros e a equação pode ser fatorada facilmente.
Exemplo de equação com raízes repetidas: x²
-4x + 4 = 0. A fatoração resulta em (x – 2)² = 0, com raiz repetida x = 2.
Interpretação Geométrica da Fatoração, Equação Do 2 Grau Como Fazer Pelo Metodo Fatoração Exemplo

Graficamente, uma equação do segundo grau representa uma parábola. As raízes da equação correspondem aos pontos onde a parábola intercepta o eixo x. A concavidade da parábola é determinada pelo sinal do coeficiente a: se a > 0, a parábola abre para cima; se a < 0, a parábola abre para baixo. O vértice da parábola representa o ponto de máximo ou mínimo da função.
Uma parábola representando uma equação do segundo grau com raízes reais e distintas interceptará o eixo x em dois pontos distintos, correspondentes às duas raízes da equação. A parábola terá um ponto de mínimo (se a > 0) ou máximo (se a < 0) no seu vértice, e a sua forma será simétrica em relação a uma reta vertical que passa pelo vértice. Por exemplo, a parábola que representa a equação x² -5x + 6 = 0, interceptará o eixo x nos pontos (2,0) e (3,0), correspondentes às raízes x = 2 e x = 3. A concavidade será voltada para cima, pois a > 0, e o vértice estará localizado no ponto (2.5, -0.25).
Dominar a fatoração de equações do segundo grau é uma conquista significativa na jornada matemática. Este método, além de eficiente, proporciona uma compreensão profunda da relação entre os coeficientes da equação e suas raízes. De equações simples a casos mais complexos, a prática constante e a aplicação dos passos demonstrados aqui te levarão à proficiência. Lembre-se: a matemática é uma ciência construída passo a passo, e cada equação resolvida é um degrau a mais rumo ao domínio completo do assunto. Agora, com os conhecimentos adquiridos, você está pronto para enfrentar qualquer desafio que envolva equações do segundo grau! Continue explorando e aprofundando seus conhecimentos matemáticos. O mundo da matemática é vasto e cheio de descobertas fascinantes!

