Escreva Três Exemplos De Divisão De Um Número Natural é um conceito fundamental na matemática, que nos permite dividir um número natural em partes iguais. A divisão é uma operação essencial em diversas áreas da vida, desde tarefas simples do dia a dia até cálculos complexos em campos como engenharia e finanças.
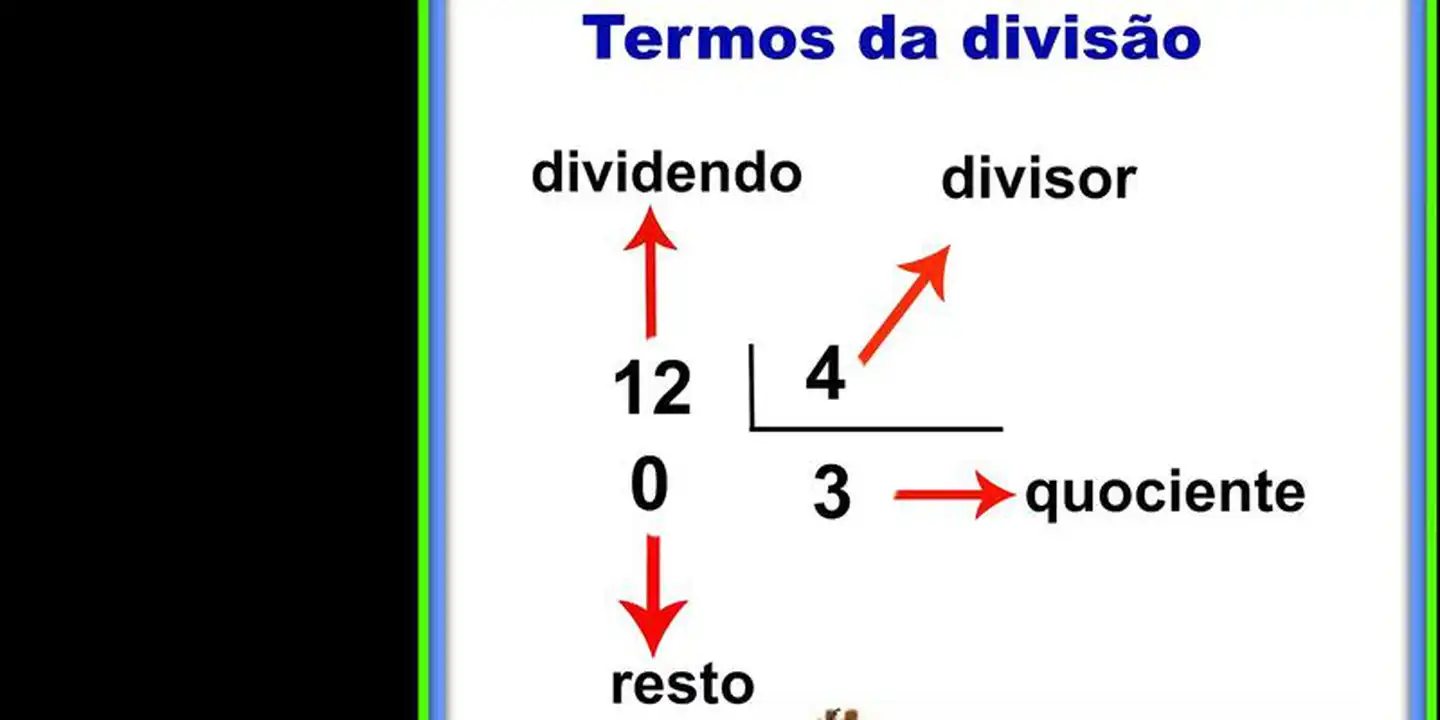
A divisão de números naturais envolve quatro elementos principais: o dividendo, o divisor, o quociente e o resto. O dividendo é o número que será dividido, o divisor é o número pelo qual o dividendo será dividido, o quociente é o resultado da divisão e o resto é o valor que sobra após a divisão.
Para compreender melhor a divisão, podemos analisar exemplos práticos, como dividir um bolo entre amigos, calcular o preço de um produto por unidade ou determinar a quantidade de material necessária para uma construção.
Introdução à Divisão de Números Naturais
A divisão é uma operação matemática fundamental que nos permite dividir um número natural em partes iguais. É uma operação essencial em diversas áreas da vida, desde cálculos simples do dia a dia até problemas complexos de engenharia e ciência.A divisão é representada pelo símbolo “÷” ou por uma barra horizontal “/”.
Ela envolve dois números: o dividendo, que é o número que será dividido, e o divisor, que é o número pelo qual o dividendo será dividido. O resultado da divisão é chamado de quociente, e o número que sobra é chamado de resto.
Partes Envolvidas na Divisão
A divisão de números naturais envolve quatro partes principais:
- Dividendo:O número que será dividido.
- Divisor:O número pelo qual o dividendo será dividido.
- Quociente:O resultado da divisão, que representa quantas vezes o divisor cabe no dividendo.
- Resto:O número que sobra após a divisão, caso o dividendo não seja divisível pelo divisor.
Por exemplo, na divisão de 15 por 3, temos:
- Dividendo: 15
- Divisor: 3
- Quociente: 5 (pois 3 cabe 5 vezes em 15)
- Resto: 0 (pois 15 é divisível por 3)
Exemplos do Dia a Dia, Escreva Três Exemplos De Divisão De Um Número Natural
A divisão é uma operação presente em diversos problemas do dia a dia, como:
- Dividir um bolo entre amigos:Se você tem um bolo com 12 fatias e quer dividir igualmente entre 4 amigos, cada amigo receberá 3 fatias (12 ÷ 4 = 3).
- Calcular a média de notas:Se você teve as seguintes notas em um semestre: 8, 7, 9 e 10, para calcular a média, você soma as notas (8 + 7 + 9 + 10 = 34) e divide pelo número de notas (34 ÷ 4 = 8,5).
- Distribuir igualmente um grupo de pessoas:Se você tem 20 pessoas e precisa dividi-las em grupos de 5 pessoas, você terá 4 grupos (20 ÷ 5 = 4).
Exemplos de Divisão de um Número Natural
Agora que já entendemos o conceito de divisão, vamos ver alguns exemplos práticos para fixar o aprendizado.
Exemplos de Divisão
Para ilustrar melhor o processo de divisão, vamos analisar três exemplos distintos, cada um com seus próprios valores para o dividendo, divisor, quociente e resto.
| Dividendo | Divisor | Quociente | Resto |
|---|---|---|---|
| 15 | 3 | 5 | 0 |
| 23 | 5 | 4 | 3 |
| 36 | 7 | 5 | 1 |
Métodos de Divisão
A divisão é uma operação matemática fundamental que nos permite dividir um número natural (o dividendo) em partes iguais, definidas por outro número natural (o divisor). Existem diferentes métodos para realizar a divisão, cada um com suas próprias vantagens e desvantagens.
Vamos explorar os principais métodos de divisão de números naturais.
Divisão em Colunas
A divisão em colunas é um método tradicional e sistemático para realizar a divisão. Ele é baseado na decomposição do dividendo em partes que são então divididas pelo divisor. O resultado final é o quociente, que representa o número de vezes que o divisor cabe no dividendo.
A divisão em colunas é um método eficaz para realizar divisões complexas, especialmente quando o divisor tem mais de um dígito.
Para realizar a divisão em colunas, siga estes passos:
- Escreva o dividendo e o divisor em uma disposição específica, com o divisor à esquerda e o dividendo à direita de um símbolo de divisão.
- Determine o maior múltiplo do divisor que é menor ou igual ao primeiro dígito do dividendo. Anote esse múltiplo abaixo do primeiro dígito do dividendo.
- Subtraia o múltiplo do primeiro dígito do dividendo.
- Baixe o próximo dígito do dividendo para formar um novo número.
- Repita os passos 2 a 4 até que não haja mais dígitos no dividendo.
- O número que você escreveu acima do dividendo é o quociente, e o número que você obteve após a última subtração é o resto.
Exemplo:Vamos dividir 75 por 5 usando a divisão em colunas:“` 15
| 75
5
25
25
0“`Neste exemplo, o quociente é 15 e o resto é 0.
Divisão por Estimativa
A divisão por estimativa é um método mais intuitivo e flexível para realizar a divisão. Ele envolve estimar o quociente, multiplicando o divisor pelo quociente estimado e comparando o resultado com o dividendo.
A divisão por estimativa é um método útil para realizar divisões rápidas, especialmente quando não é necessário obter um resultado preciso.
Para realizar a divisão por estimativa, siga estes passos:
- Estime o quociente, considerando o divisor e o dividendo.
- Multiplique o divisor pelo quociente estimado.
- Compare o resultado com o dividendo.
- Se o resultado for menor que o dividendo, aumente o quociente estimado. Se o resultado for maior que o dividendo, diminua o quociente estimado.
- Repita os passos 2 a 4 até que o resultado seja próximo ou igual ao dividendo.
- O quociente estimado final é o quociente da divisão.
Exemplo:Vamos dividir 75 por 5 usando a divisão por estimativa:
- Sabemos que 5 x 10 = 50, e 5 x 15 = 75. Portanto, podemos estimar que o quociente é 15.
- Multiplicamos 5 x 15 = 75.
- O resultado é igual ao dividendo, então o quociente estimado é o quociente da divisão.
Divisão por Frações
A divisão por frações é um método que converte a divisão em uma multiplicação de frações. Ele é útil para resolver divisões que envolvem frações ou números decimais.
A divisão por frações é um método eficiente para realizar divisões que envolvem frações ou números decimais, transformando a operação em uma multiplicação.
Para realizar a divisão por frações, siga estes passos:
- Converta o divisor em uma fração, se necessário.
- Inverter a fração do divisor.
- Multiplique o dividendo pela fração invertida do divisor.
- Simplifique a fração resultante, se possível.
Exemplo:Vamos dividir 75 por 5 usando a divisão por frações:
- Converta 5 em uma fração: 5/1.
- Inverter a fração do divisor: 1/5.
- Multiplique o dividendo pela fração invertida do divisor: 75 x (1/5) = 15.
Propriedades da Divisão
A divisão de números naturais possui algumas propriedades importantes que facilitam a realização de cálculos e a compreensão de como ela funciona. Vamos explorar algumas dessas propriedades:
Propriedade Comutativa
A propriedade comutativa da divisão não se aplica. A ordem dos números na divisão influencia o resultado. Em outras palavras, dividir um número por outro não é o mesmo que dividir o segundo número pelo primeiro.
Exemplo: 12 ÷ 4 = 3, mas 4 ÷ 12 = 1/3.
Propriedade Associativa
A propriedade associativa da divisão também não se aplica. A forma como os números são agrupados em uma divisão afeta o resultado.
Exemplo: (12 ÷ 4) ÷ 3 = 1, mas 12 ÷ (4 ÷ 3) = 9.
Propriedade Distributiva
A propriedade distributiva da divisão se aplica quando estamos dividindo uma soma por um número.
Exemplo: (10 + 6) ÷ 2 = 10 ÷ 2 + 6 ÷ 2 = 5 + 3 = 8.
Em outras palavras, podemos dividir cada parcela da soma separadamente pelo divisor e depois somar os resultados.
Aplicações da Divisão: Escreva Três Exemplos De Divisão De Um Número Natural

A divisão é uma operação matemática fundamental que está presente em diversas situações do nosso dia a dia. Ela é utilizada para dividir um todo em partes iguais, determinar a quantidade de vezes que um número cabe em outro, ou mesmo para calcular a média de um conjunto de valores.
Aplicações da Divisão no Cotidiano
A divisão é uma ferramenta essencial para resolver problemas em diversas áreas da vida, como:
- Finanças:Dividir uma conta entre amigos, calcular o valor de cada parcela de um empréstimo, determinar o lucro por unidade vendida, entre outros.
- Cozinha:Dividir uma receita para um número menor de pessoas, calcular a quantidade de ingredientes necessária para uma determinada quantidade de porções.
- Viagens:Dividir o custo total de uma viagem entre os participantes, calcular a velocidade média de um veículo, determinar o tempo necessário para percorrer uma determinada distância.
- Matemática:Resolver problemas de frações, calcular o quociente de dois números, determinar o resto da divisão, entre outros.
- Engenharia:Calcular a resistência de um material, determinar a capacidade de carga de uma estrutura, calcular a área de uma superfície, entre outros.
- Computação:Dividir um arquivo em partes menores para facilitar o download, calcular o tempo médio de processamento de um programa, determinar o tamanho de um bloco de memória, entre outros.
Exemplos de Aplicações da Divisão
- Divisão de uma conta entre amigos:Se quatro amigos saem para jantar e a conta total é de R$ 120,00, cada um deve pagar R$ 30,00 (R$ 120,00 ÷ 4 = R$ 30,00).
- Cálculo da velocidade média de um carro:Se um carro percorre 240 km em 4 horas, sua velocidade média é de 60 km/h (240 km ÷ 4 h = 60 km/h).
- Determinação do lucro por unidade vendida:Se uma empresa vende 100 unidades de um produto por R$ 1.000,00 e o custo de produção é de R$ 500,00, o lucro por unidade é de R$ 5,00 (R$ 1.000,00 ÷ 100 = R$ 10,00 – R$ 500,00 ÷ 100 = R$ 5,00).
Aplicações da Divisão em Diferentes Áreas
- Matemática:A divisão é fundamental para a resolução de problemas de frações, proporções, equações e outros conceitos matemáticos. Por exemplo, para simplificar uma fração como 4/8, dividimos o numerador e o denominador por 4, obtendo 1/2.
- Finanças:A divisão é utilizada para calcular juros, taxas de retorno, dividendos, custos de produção e outros indicadores financeiros. Por exemplo, para calcular o juros de um investimento de R$ 1.000,00 a uma taxa de 10% ao ano, dividimos o valor do investimento pela taxa de juros (R$ 1.000,00 ÷ 10% = R$ 100,00).
- Engenharia:A divisão é utilizada para calcular a força, a pressão, a velocidade, a aceleração e outros parâmetros importantes em projetos de engenharia. Por exemplo, para calcular a força necessária para levantar um objeto de 100 kg, dividimos a massa do objeto pela aceleração da gravidade (100 kg ÷ 9,8 m/s² = 10,2 kgf).
A divisão de números naturais é uma operação matemática crucial, que desempenha um papel fundamental em diversas áreas da vida. Ao dominar os diferentes métodos de divisão e compreender suas propriedades, podemos resolver problemas do dia a dia e realizar cálculos complexos com mais facilidade.
A prática e o estudo aprofundado da divisão nos permitem aprimorar nossa capacidade de raciocínio lógico e matemático, abrindo portas para novas oportunidades e desafios.

