Os Fatoriais Sao Importantes Em Analise Combinatoria. Por Exemplo – Os Fatoriais São Importantes Em Analise Combinatoria. Por Exemplo, a contagem de arranjos e combinações de objetos distintos é um problema fundamental na análise combinatória, e os fatoriais desempenham um papel crucial nesse contexto. O fatorial de um número natural n, denotado por n!, representa o produto de todos os inteiros positivos de 1 até n.
Essa função matemática fornece uma maneira eficiente de calcular o número de permutações possíveis de um conjunto de objetos distintos.
A análise combinatória, área da matemática que lida com a contagem e arranjo de objetos, encontra nos fatoriais um aliado poderoso. Os fatoriais permitem calcular de forma precisa o número de maneiras de organizar, agrupar ou selecionar elementos, tornando-se ferramentas essenciais na resolução de problemas em diversas áreas, como probabilidade, estatística, informática e até mesmo na vida cotidiana.
Introdução aos Fatoriais
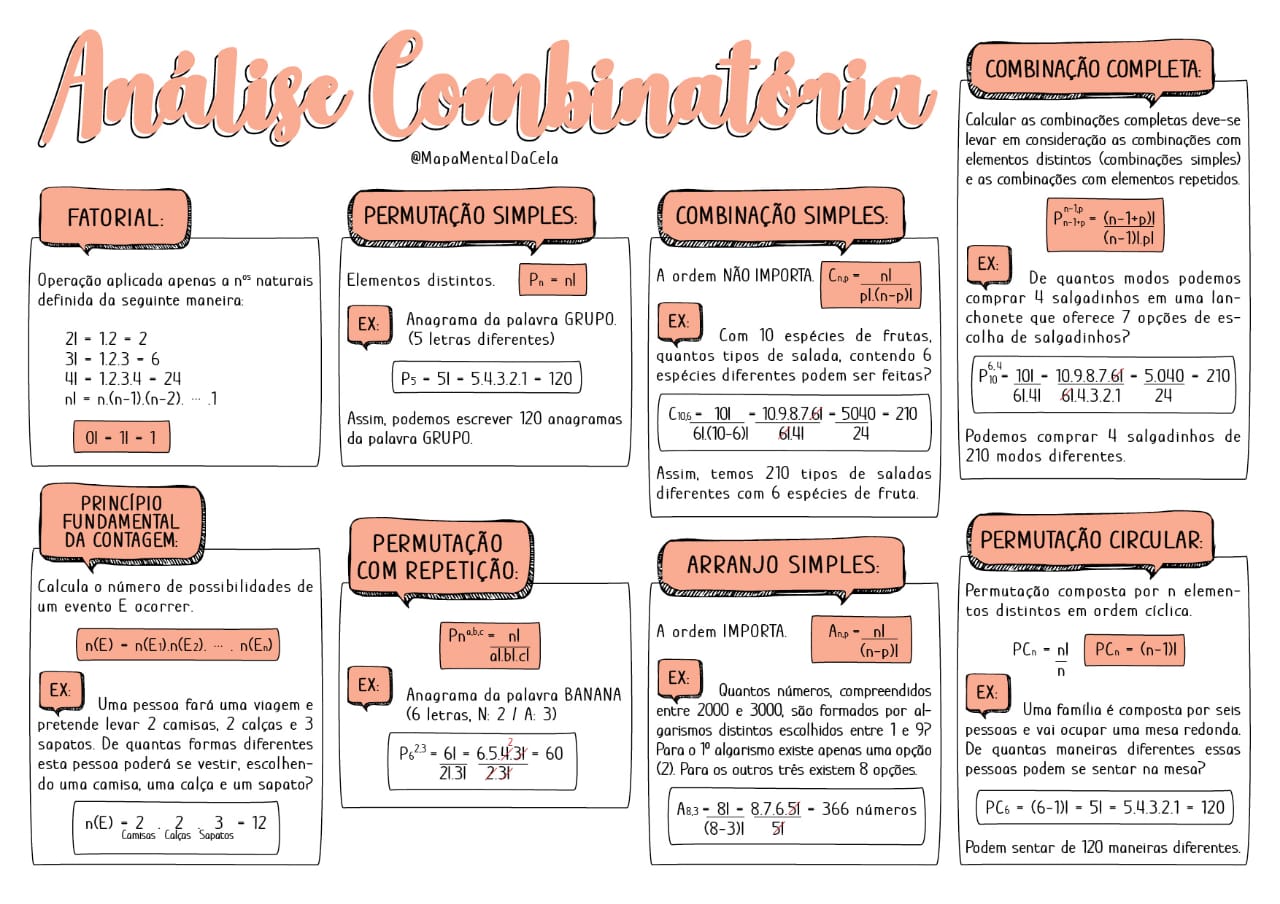
O conceito de fatorial é fundamental em análise combinatória, sendo utilizado para calcular o número de maneiras de organizar ou selecionar objetos distintos. O fatorial de um número natural
- n*, denotado por
- n*!, representa o produto de todos os números naturais de 1 até
- n*.
Definição e Representação Matemática
O fatorial de um número naturaln* é definido como o produto de todos os números naturais de 1 até
-n*. Matematicamente, isso é expresso como
n! = n
- (n
- 1)
- (n
- 2)
- …
- 2
- 1
Por exemplo, o fatorial de 5, denotado por 5!, é calculado como:
5! = 5
- 4
- 3
- 2
- 1 = 120
Aplicações Práticas de Fatoriais
Fatoriais têm diversas aplicações práticas em análise combinatória, como:* Permutações:O número de maneiras de organizar
- n* objetos distintos em uma sequência é dado por
- n*!. Por exemplo, o número de maneiras de organizar 4 pessoas em uma fila é 4! = 24.
- k* objetos distintos de um conjunto de
- n* objetos, sem levar em consideração a ordem, é dado por n! / (k!
- (n
- k)!). Por exemplo, o número de maneiras de escolher 2 pessoas de um grupo de 5 é 5! / (2!
- 3!) = 10.
Combinações
O número de maneiras de escolher
Probabilidade
Fatoriais são utilizados para calcular probabilidades em eventos que envolvem arranjos ou escolhas de objetos. Por exemplo, a probabilidade de tirar uma carta específica de um baralho de 52 cartas é 1/52!.
Comparação com Outras Operações Matemáticas
O cálculo de fatoriais difere de outras operações matemáticas como adição, subtração, multiplicação e divisão. Enquanto essas operações são realizadas com dois ou mais números, o fatorial é aplicado a um único número. Além disso, o fatorial cresce rapidamente à medida que o número aumenta, tornando-o uma operação complexa para números grandes.
Fatoriais na Análise Combinatória
Fatoriais desempenham um papel crucial na análise combinatória, fornecendo uma ferramenta poderosa para contar e organizar arranjos e combinações de elementos distintos. Eles são utilizados em diversas áreas da análise combinatória, como permutações, combinações e arranjos com repetição.
Aplicações de Fatoriais na Análise Combinatória
Fatoriais são ferramentas essenciais para resolver problemas que envolvem a contagem de arranjos e combinações de objetos.
- Permutações: Uma permutação é uma ordenação de elementos distintos. O número de permutações de -n* elementos distintos é dado por -n*!. Por exemplo, o número de maneiras de ordenar 5 livros distintos em uma estante é 5! = 120.
- Combinações: Uma combinação é um grupo de elementos distintos, onde a ordem não importa. O número de combinações de -n* elementos distintos tomados -k* de cada vez é dado por nCk = n! / (k! – (n-k)!). Por exemplo, o número de maneiras de escolher 3 livros de um conjunto de 5 livros distintos é 5C3 = 5! / (3! – 2!) = 10.
- Arranjos com Repetição: Um arranjo com repetição é uma ordenação de elementos, onde a repetição é permitida. O número de arranjos com repetição de -n* elementos distintos tomados -k* de cada vez é dado por n^k. Por exemplo, o número de maneiras de formar uma senha de 4 dígitos usando os dígitos 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9 é 10^4 = 10.000.
Exemplos de Problemas
- De quantas maneiras 8 pessoas podem se sentar em uma mesa redonda? (Permutações circulares: (n-1)!)
- De quantas maneiras podemos escolher um time de 5 jogadores de um grupo de 10 jogadores? (Combinações: nCk)
- Quantos anagramas podem ser formados com a palavra “BANANA”? (Arranjos com repetição: n! / (n1! – n2! – … – nk!))
Tabela de Problemas Combinatórios e Fórmulas, Os Fatoriais Sao Importantes Em Analise Combinatoria. Por Exemplo
| Problema | Fórmula | Exemplo |
|---|---|---|
| Permutações | n! | Número de maneiras de ordenar 5 livros: 5! = 120 |
| Combinações | nCk = n! / (k!
|
Número de maneiras de escolher 3 livros de 5: 5C3 = 10 |
| Arranjos com Repetição | n^k | Número de senhas de 4 dígitos: 10^4 = 10.000 |
Permutações: Os Fatoriais Sao Importantes Em Analise Combinatoria. Por Exemplo

Uma permutação é um arranjo ordenado de objetos distintos. Em outras palavras, uma permutação é uma forma de escolher e organizar um grupo de objetos, levando em consideração a ordem em que eles são escolhidos.
Os fatoriais desempenham um papel crucial no cálculo do número de permutações possíveis.
Permutações Sem Repetição
As permutações sem repetição ocorrem quando nenhum objeto pode ser usado mais de uma vez em um arranjo. Por exemplo, se tivermos três objetos distintos (A, B e C), o número de permutações possíveis sem repetição é 3! (3 fatorial), que é 3
- 2
- 1 = 6.
- ABC
- ACB
- BAC
- BCA
- CAB
- CBA
Em geral, o número de permutações sem repetição de
- n* objetos distintos é dado por
- n*!.
Permutações Com Repetição
As permutações com repetição ocorrem quando alguns objetos são idênticos. Por exemplo, se tivermos a palavra “BANANA”, que tem 6 letras, mas com algumas letras repetidas, o número de permutações possíveis é diferente do caso sem repetição. Para calcular o número de permutações com repetição, usamos a seguinte fórmula:
n! / (n1!
- n2!
- …
- nk!)
Onde:*
- n* é o número total de objetos
- n1*,
- n2*, …,
- nk* são os números de repetições de cada objeto.
No exemplo da palavra “BANANA”, temos:*
- n* = 6 (total de letras)
- n1* = 3 (repetições da letra “A”)
- n2* = 2 (repetições da letra “N”)
- n3* = 1 (repetições da letra “B”)
Portanto, o número de permutações possíveis da palavra “BANANA” é:
- ! / (3!
- 2!
- 1!) = 720 / (6
- 2
- 1) = 60
Fórmula de Permutação
A fórmula de permutação é uma expressão matemática que permite calcular o número de permutações possíveis de um conjunto de objetos. A fórmula é dada por:
nPr = n! / (n
r)!
Onde:*
- n* é o número total de objetos
- r* é o número de objetos escolhidos para a permutação
Essa fórmula é válida para permutações sem repetição. Se houver repetições, a fórmula deve ser modificada de acordo com o número de repetições de cada objeto, como descrito na seção anterior.
Combinações
Em análise combinatória, combinações referem-se ao número de maneiras de escolher um grupo de elementos de um conjunto maior, sem levar em consideração a ordem dos elementos escolhidos. Por exemplo, se você tem um conjunto de 5 frutas e deseja escolher 3 delas, não importa a ordem em que você as escolhe, apenas o grupo final de 3 frutas.
Combinações são frequentemente usadas em problemas de probabilidade, estatística e outros campos.
Relação com Fatoriais
Fatoriais desempenham um papel crucial na fórmula de combinação. Um fatorial de um número inteiro positivo n, denotado por n!, é o produto de todos os inteiros positivos menores ou iguais a n. Por exemplo, 5! = 5 × 4 × 3 × 2 × 1 = 120.
A fórmula de combinação utiliza fatoriais para calcular o número de maneiras de escolher um grupo de elementos, levando em consideração o número total de elementos e o número de elementos a serem escolhidos.
Exemplos de Problemas que Envolvem Combinações
Combinações são amplamente aplicadas em diversas situações da vida real. Aqui estão alguns exemplos:
- Um grupo de 10 pessoas deseja formar um comitê de 3 membros. Quantas combinações de comitês são possíveis?
- Um jogador de pôquer recebe 5 cartas de um baralho de 52 cartas. Quantas combinações diferentes de mãos de pôquer são possíveis?
- Uma loja de sorvetes oferece 10 sabores diferentes. Quantas combinações de 3 sabores são possíveis?
Fórmula de Combinação
A fórmula de combinação é utilizada para calcular o número de combinações possíveis de um conjunto de elementos. Ela é dada por:
nCr = n! / (r!
- (n
- r)!)
Onde:
- nCr representa o número de combinações possíveis de r elementos escolhidos de um conjunto de n elementos.
- n é o número total de elementos no conjunto.
- r é o número de elementos a serem escolhidos.
Cálculo do Número de Grupos Possíveis
Para ilustrar como a fórmula de combinação é aplicada, vamos considerar o exemplo do comitê de 3 membros formado por um grupo de 10 pessoas. Usando a fórmula de combinação, podemos calcular o número de combinações possíveis:
- C3 = 10! / (3!
- (10
- 3)!) = 10! / (3!
- 7!) = (10 × 9 × 8) / (3 × 2 × 1) = 120
Portanto, existem 120 combinações possíveis de comitês de 3 membros que podem ser formados a partir de um grupo de 10 pessoas.
Aplicações Práticas dos Fatoriais

Os fatoriais, além de sua importância na análise combinatória, possuem aplicações práticas em diversas áreas, como probabilidade, estatística e informática. Eles são ferramentas essenciais para a resolução de problemas que envolvem contagem, permutações e combinações, sendo utilizados em áreas como criptografia, análise de dados e desenvolvimento de algoritmos.
Aplicações em Probabilidade e Estatística
Os fatoriais são fundamentais para o cálculo de probabilidades em eventos que envolvem arranjos e combinações. Por exemplo, na probabilidade de se obter uma sequência específica de cartas em um baralho, o fatorial é utilizado para determinar o número total de possíveis sequências.
Em estatística, os fatoriais são utilizados em testes de hipóteses, análise de variância e outros métodos estatísticos.
O fatorial de um número natural
- n*, denotado por
- n*!, é o produto de todos os inteiros positivos de 1 até
- n*.
Aplicações em Informática
Os fatoriais são utilizados em algoritmos de ordenação, como o algoritmo de ordenação por bolha e o algoritmo de ordenação por inserção. Eles também são utilizados em algoritmos de busca, como o algoritmo de busca binária. Em criptografia, os fatoriais são utilizados em algoritmos de criptografia de chave pública, como o algoritmo RSA.
O fatorial de um número
-n* é calculado como
- n*! =
- n*
- (n-1)
- (n-2)
- …
- 2
- 1.
Exemplo de Aplicação
Imagine um cenário em que uma empresa precisa organizar um evento com 10 palestrantes. A empresa deseja determinar o número de maneiras diferentes que os palestrantes podem ser organizados na ordem de apresentação. Utilizando o fatorial, podemos calcular o número de permutações possíveis: 10! = 10
- 9
- 8
- 7
- 6
- 5
- 4
- 3
- 2
- 1 = 3.628.800.
Q&A
Como calcular o fatorial de um número?
O fatorial de um número natural n, denotado por n!, é calculado multiplicando todos os inteiros positivos de 1 até n. Por exemplo, 5! = 5 – 4 – 3 – 2 – 1 = 120.
Qual a diferença entre permutação e combinação?
Uma permutação é um arranjo ordenado de objetos, enquanto uma combinação é um grupo não ordenado de objetos. Em uma permutação, a ordem dos objetos importa, enquanto em uma combinação, a ordem não importa.
Quais são as principais aplicações dos fatoriais na vida real?
Os fatoriais têm diversas aplicações práticas, como na contagem de senhas, na análise de dados estatísticos, na programação de computadores, na criptografia e em diversas outras áreas da ciência e da tecnologia.

